[物理] 物体の同士の衝突
物体同士が衝突したときの動きについてのメモ書きです。
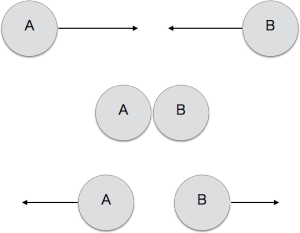
例えば、以下のように物体A、Bが衝突したとします。
衝突後の物体A、Bの動きについて考えてみたいと思います。
衝突は上のように真正面から衝突するパターンはまれで斜めから衝突する場面が大半でしょう。
しかし、簡単のため真正面の場合で考えたいと思います。
物体A、Bの質量を、
、速度を
、
とします。
このとき、運動量保存の法則により以下の関係式が成り立ちます。
上記の、
を求めることが今回の目的です。
物体同士が衝突するとき、弾性係数eにより以下のように表現できます。
これは衝突前と衝突後の物体Aに対する物体Bの相対速度の比です。
eの取りうる範囲はです。
ここで、式1、2で連立方程式が立つため、自然と、
が解けることになります。
実際に解いてみると以下の答えが求まります。
これで真正面からの物体の衝突の動きを求めることができました。
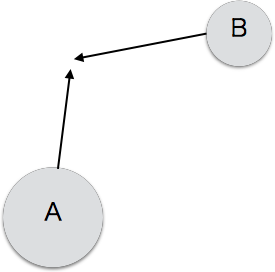
この応用として任意の向きで物体A、Bが衝突する場合も考えてみます。
基本的な考え方はxyz成分でベクトル分解し、それぞれのベクトル上での2物体の正面衝突とすることです。
したがって、以下のベクトルの方程式が導かれます。
各成分の正面衝突には上の答えがそのまま適用できます。
これで斜めのパターンについも動きが求められました。

![[お知らせ] 活動再開、そして2021年に向けて](https://ftvoid.com/blog/wp-content/uploads/2018/09/profile-250x154.png)
![[お知らせ] 独りゲームジャムをやります](https://ftvoid.com/blog/wp-content/themes/dp-colors/img/post_thumbnail/noimage.png)