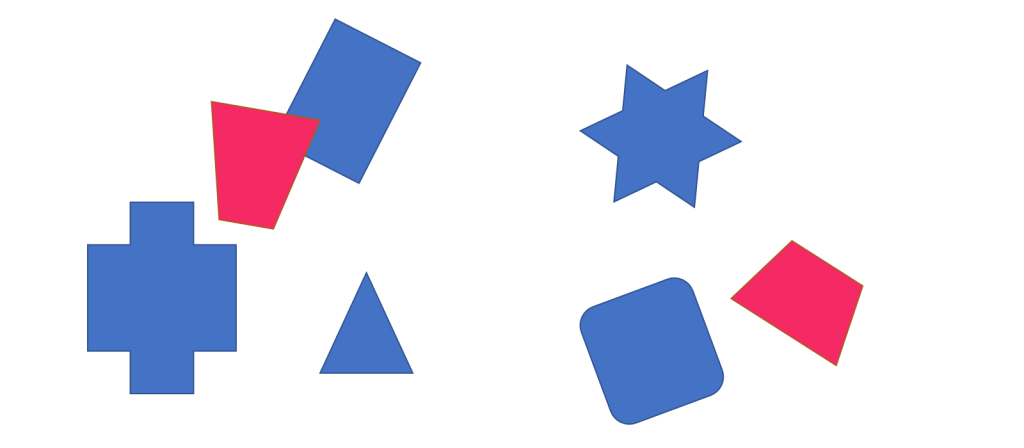
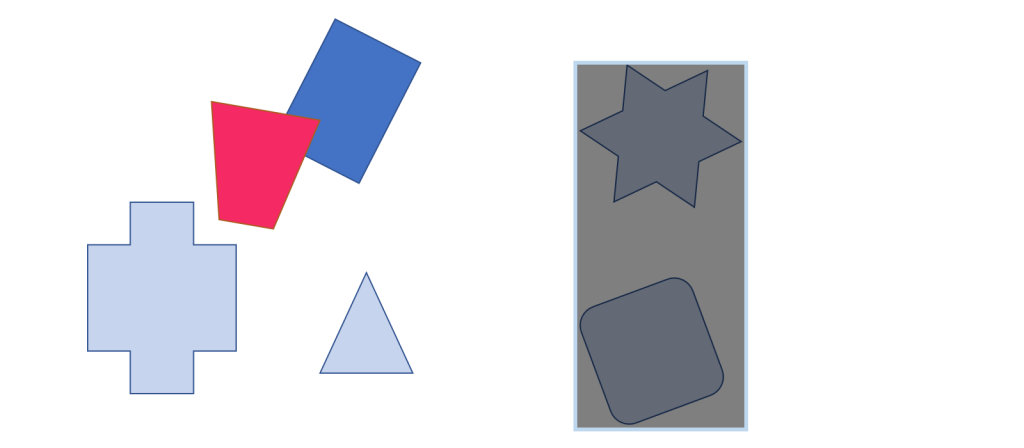
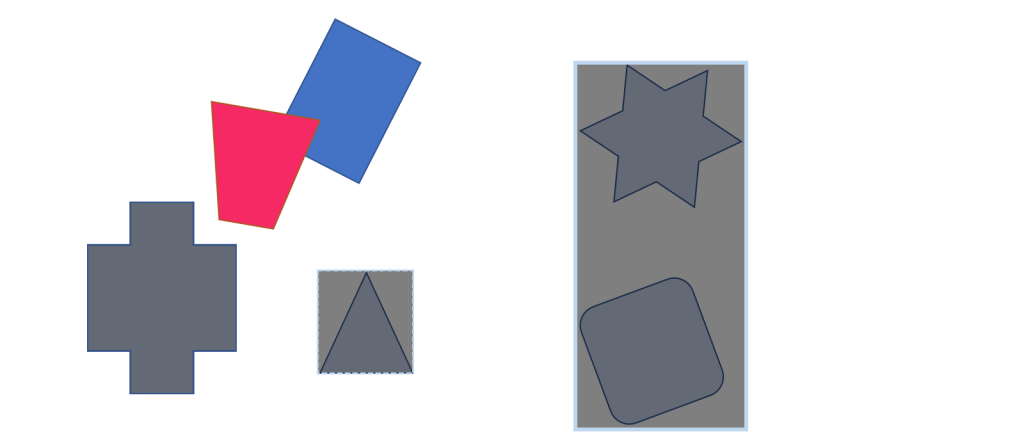
以下の様に多数のオブジェクト同士の当たり判定を考えます。

ここで、赤色と青色のオブジェクトをそれぞれA、Bのグループに分類します。
当たり判定はグループA、B同士で行うこととします。

グループA、Bのオブジェクトの個数をそれぞれNa、Nbとすると、
当たり判定の総実行回数はNa×Nbとなります。

例えば、Na=100、Nb=200の場合、100×200=20000回の当たり判定を行わなければなりません。
このままでは非常に処理コストがかかってしまいます。

この当たり判定回数を減らす方法はないのでしょうか？

この解決方法の一つにAABB木を用いる方法があります。
AABBとはAxis-Aligned Bounding Boxの略で直訳すると軸平行境界ボックスとなります。
要はxy座標軸に平行な辺の矩形、言い換えれば回転したり歪んだりしていない矩形の領域のことを指します。

AABB木とは、AABBの中にさらにAABBを入れ子状態にして表現したものです。
通常はAABBの中に最大2個の子AABBを持つようにします。

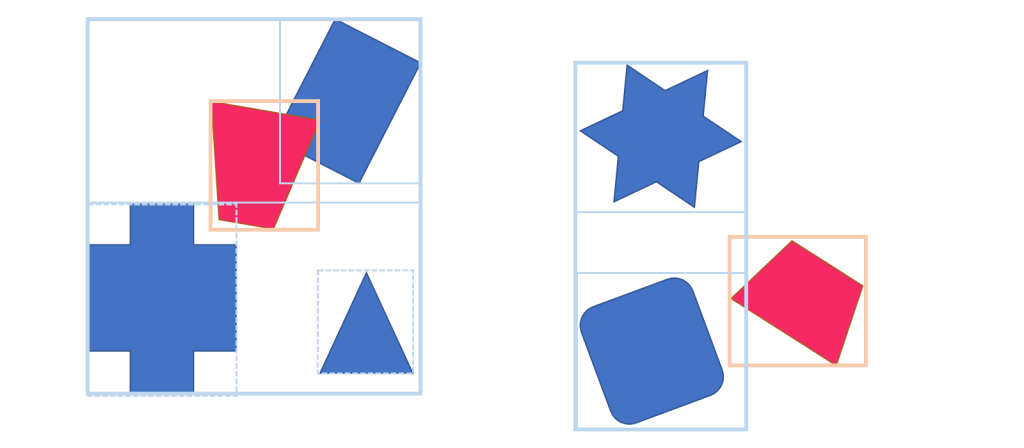
グループA、BをAABBで分割すると以下の様になります。

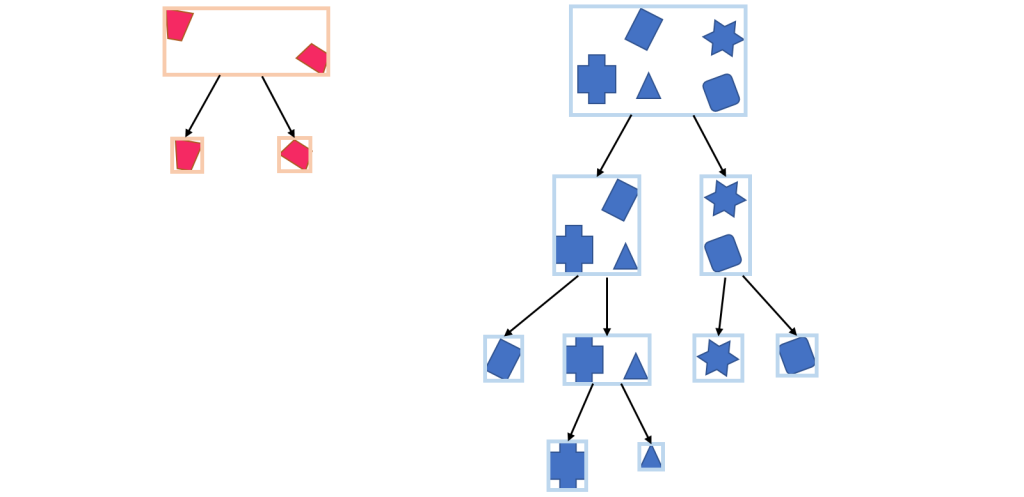
このAABBは以下のような木構造で管理されます。

木構造の末端は必ずオブジェクトが1個になるようにします。

この木構造は探索木になっているため、
不要な探索(=当たり判定)を大幅に削減することができます。

これをグループA、Bの当たり判定に適用すると、判定回数は最小でNa×log(Nb)またはlog(Na)×Nbまで減らせます。
この式から、オブジェクトの多い個数に対してlogを取った方が当たり判定回数を減らせることが分かります。

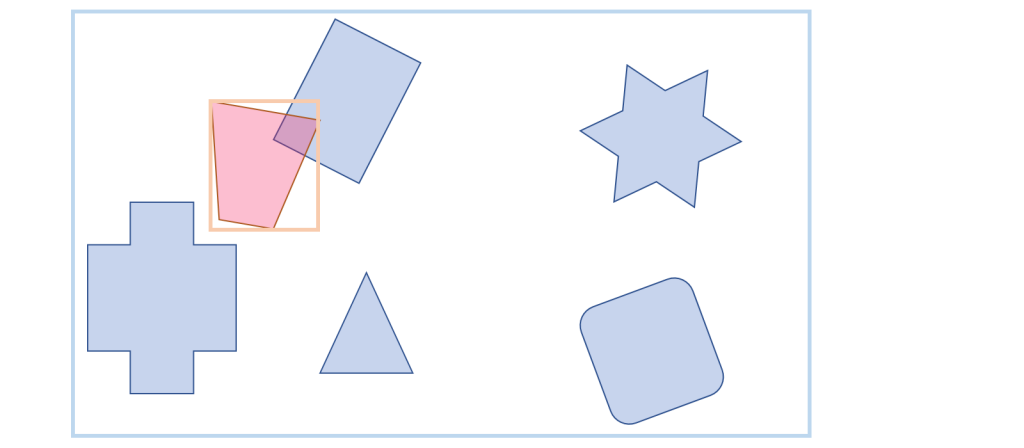
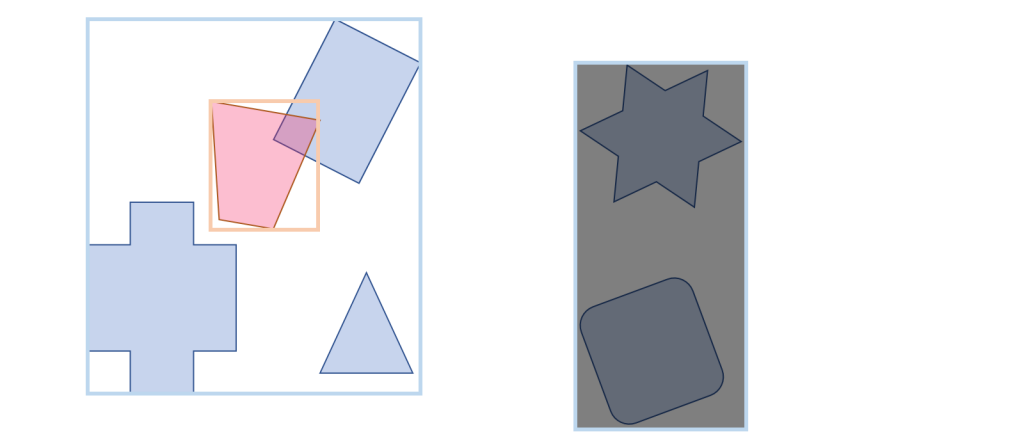
では、あるグループAのオブジェクトOaとグループBのオブジェクト全体との当たり判定の動作を見てみましょう。

OaのAABBとグループBのルートノードのAABBとの当たり判定を行います。

ルートノードはゲームで言うマップエリア全体の矩形などに設定されます。
そのため、ほぼ当たりとなります。

次に、ルートノードの小ノードのAABBとの当たり判定を行います。
小ノードは2つあります。

OaのAABBは小ノードの両方に重なる可能性があるため、
すべての小ノードとの当たり判定を行います。

上図の場合、図の左側のノードのAABBのみが「当たり」となりました。
これでもう一方の図の右側のノードのAABBにあるグループBのオブジェクトはすべて「はずれ」となります。
したがって、左側のノードのみ調べれば良いです。

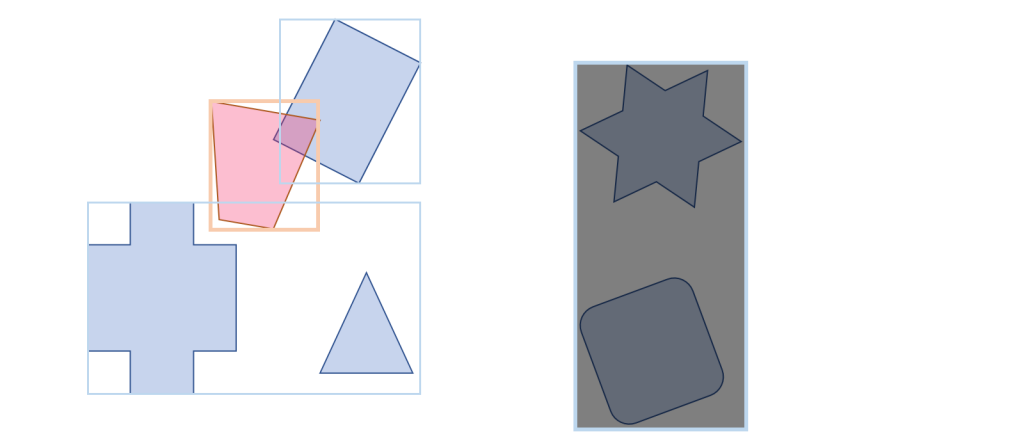
引き続き更なる小ノードのAABBを調べます。

今度は両方とも「当たり」となりました。
したがって、両方の小ノード以下の当たり判定を行う必要があります。

まず、上側のノード以下を調べます。
このノードには小ノードがありません。
したがって、これはグループBのオブジェクトとなります。

Oaと重なっているため、詳細な当たり判定(ナローフェーズ)を行います。

図より明らかに重なっていることがわかります。

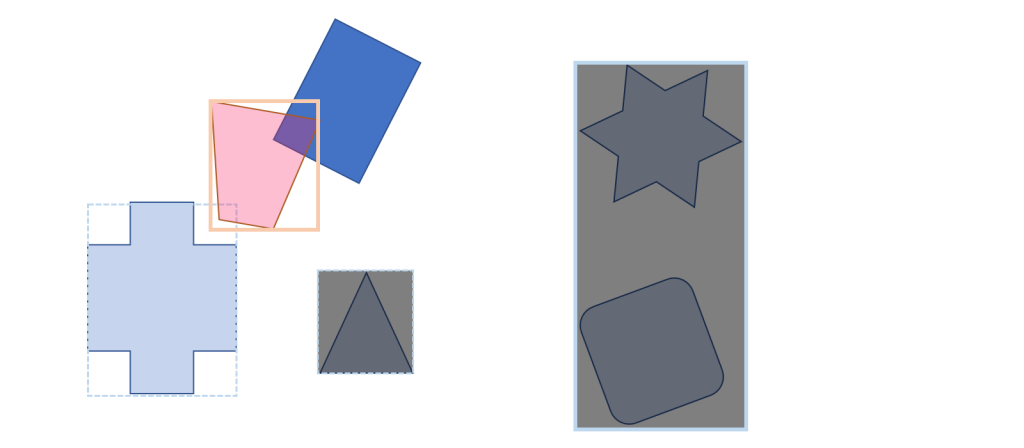
この当たり判定が終わったら、ノードを遡って次のノードのAABBを調べます。

この例では左側ノードのAABBのみ「当たり」です。
また、このノードは小ノードを持たないためグループBのオブジェクトとなります。
ここで詳細な当たり判定を実行します。

今度は「はずれ」になりました。

これでもう調べるノードが無くなりました。
当たり判定はこれで終了です。

今回の例ではあまり効果が見込めませんが、
オブジェクトの数が多くなるほどAABB木を用いたほうが劇的に判定回数が少なくなります。
そのため、多数のオブジェクト同士との当たり判定を行うのには欠かせない方法でしょう。

このように、AABB木は多数のオブジェクトの当たり判定で真価を発揮しますが欠点も存在します。
それは、オブジェクトが移動した場合です。
もしグループBのオブジェクトが移動した場合、AABB木を再構築しなければなりません。

AABB木作成の処理コストもオブジェクトの数が増えるほど無視できなくなるため、
静的なオブジェクトに対して適用する程度にとどめておいたほうが良いかもしれませんね。

■参考書籍
藤澤 誠(2013)『CGのための物理シミュレーションの基礎』マイナビ