2Dゲームにおける基本図形の当たり判定

2Dゲームでよく使用すると思われる図形の当たり判定計算のまとめです。

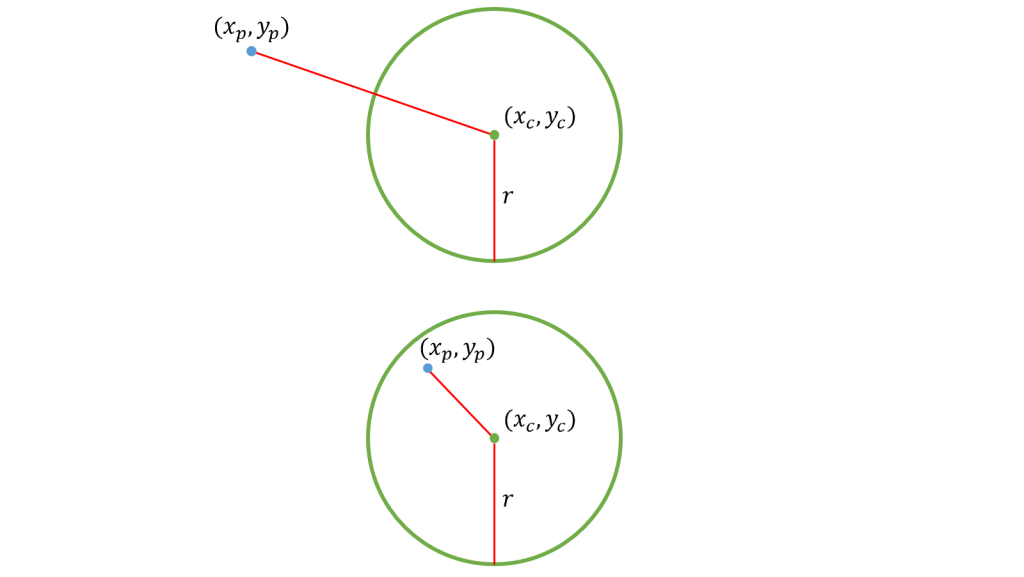
■点と円
点と円の中心との距離が円の半径より小さくなると当たりとなります。

したがって、計算式は以下のようになります。

$\sqrt{(x_{p}-x_{c})^2+(y_{p}-y_{c})^2} < r$

しかし、左辺には平方根を用いておりパフォーマンスが悪いので、通常は両辺を二乗した次式を用います。

$(x_{p}-x_{c})^2+(y_{p}-y_{c})^2 < r^2$

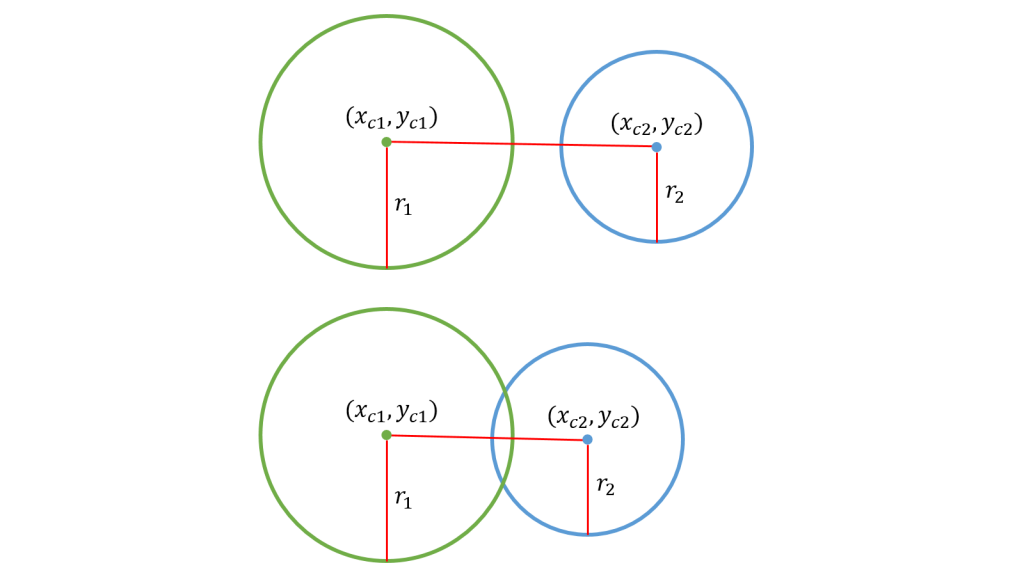
■円と円
２つの円の中心点との距離が２つの円の半径の総和より小さくなると当たりとなります。

これも点と円の当たり判定同様、両辺を二乗した式を用います。
したがって、計算式は以下のようになります。

$(x_{c1}-x_{c2})^2+(y_{c1}-y_{c2})^2 < (r_{1}+r_{2})^2$

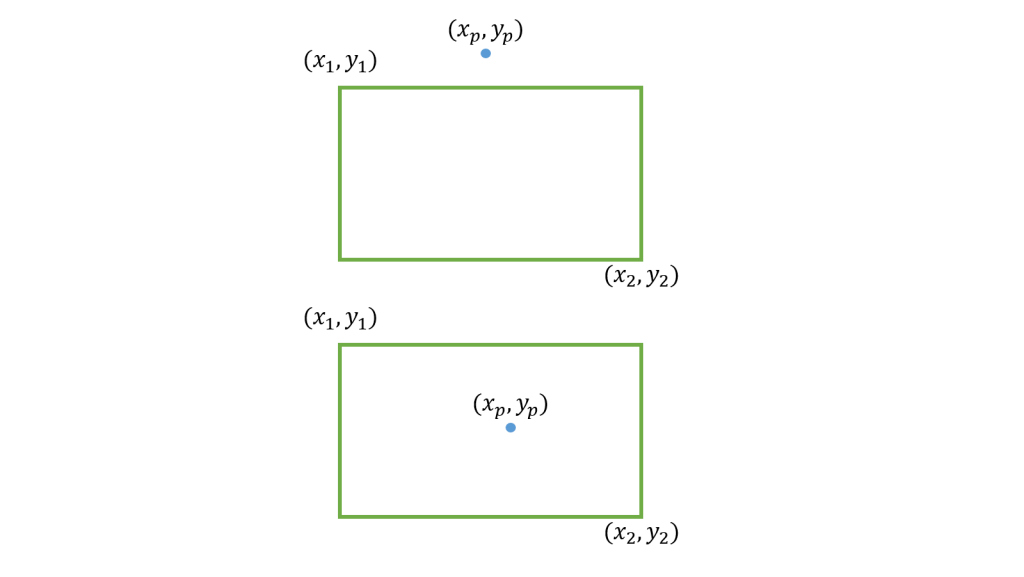
■点と長方形
点が長方形の左辺と右辺の間、且つ上辺と底辺の間にあるときに当たりとなります。

したがって、計算式は以下のようになります。

$(x_{p} > x_{1}) \land (x_{p} < x_{2}) \land (y_{p} > y_{1}) \land (y_{p} < y_{2})$

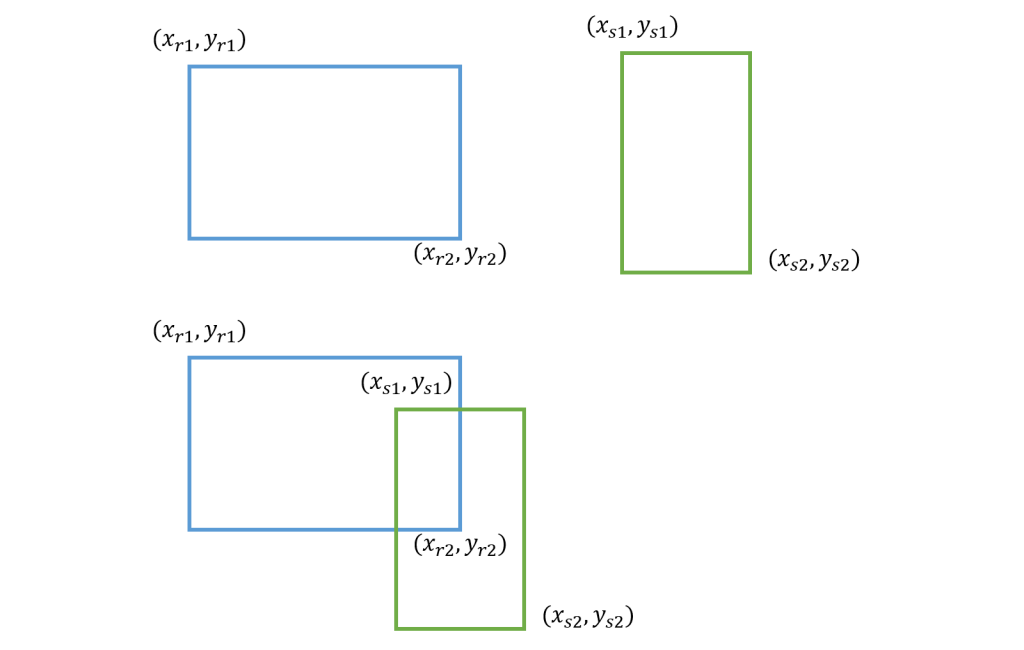
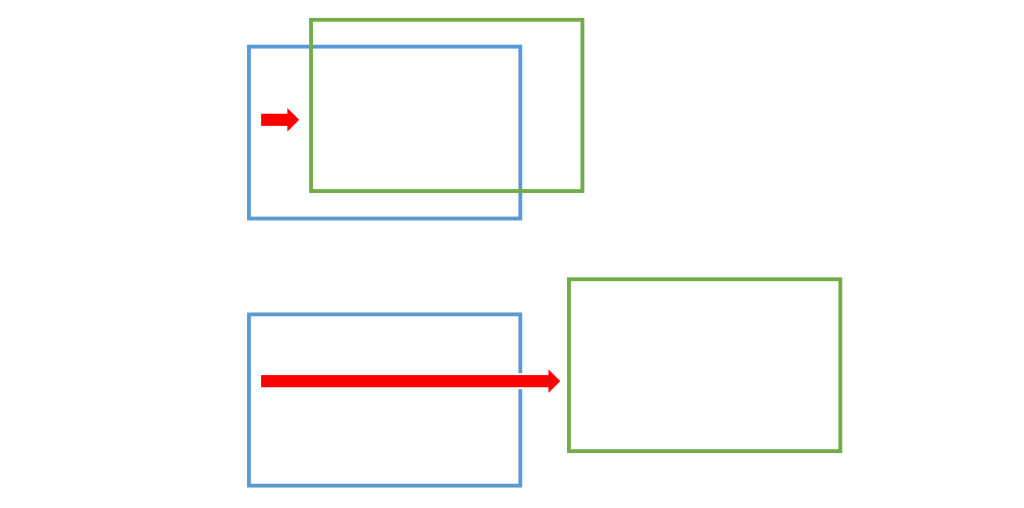
■長方形と長方形

まず、x軸方向のみで考えます。
長方形同士が重なるためには、長方形1の右辺が長方形2の左辺より大きくなる必要があります。

しかし、このままでは長方形1の左辺が長方形2の右辺以上になった場合ははずれてしまいます。
したがって、長方形1の左辺が長方形2の右辺より小さくなる必要があります。
これはy軸方向に対しても言えます。
最終的な計算式は以下のようになります。

$(x_{r2} > x_{s1}) \land (x_{r1} < x_{s2}) \land (y_{r2} > y_{s1}) \land (y_{r1} < y_{s2})$

4種類の当たり判定を挙げましたが、どれも非常によく使うと思われる当たり判定です。
他のサイト様でも詳しく解説されているので需要が無いと思われますが、おさらいを兼ねてのまとめでした。

ftvlog