今回は2Dゲームにおける円と長方形の当たり判定計算についてです。

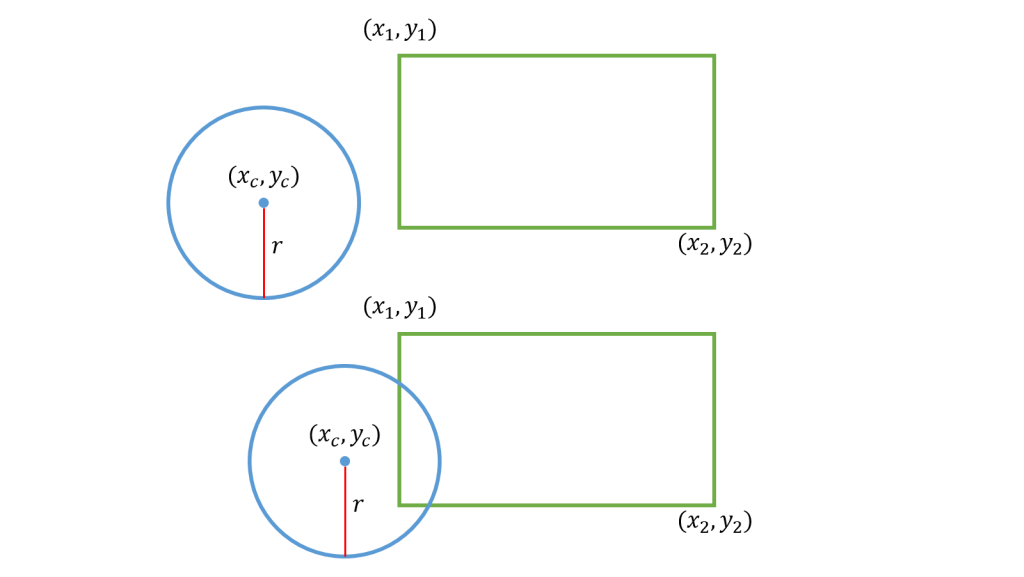
基本的な考え方は、円が長方形と重なるような円の中心点の領域をチェックするイメージです。
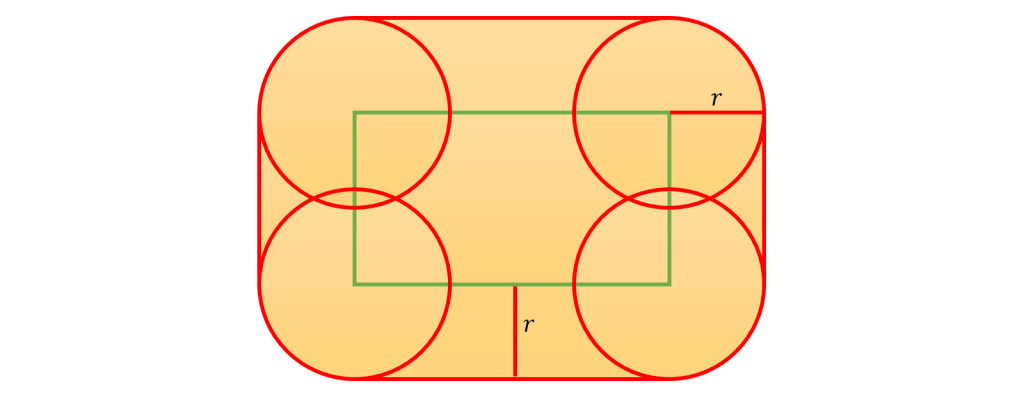
これは以下の角丸長方形の領域となります。

円の中心点がこの領域に入っているかどうかをチェックします。

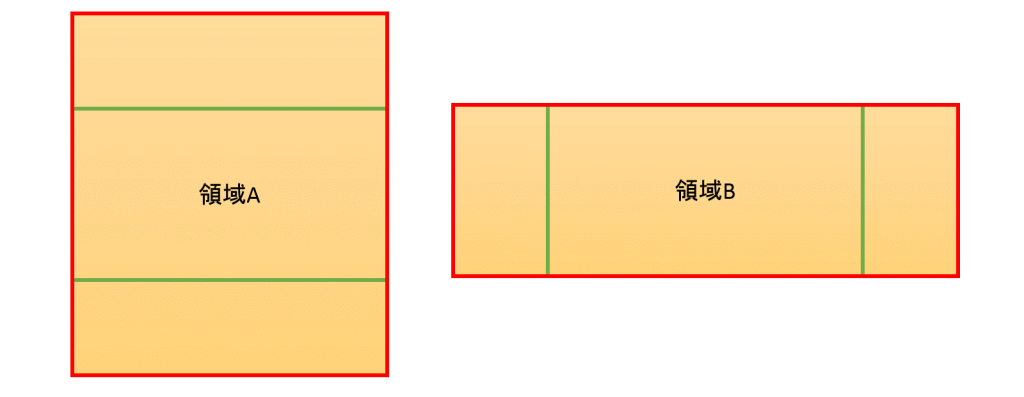
まず、以下の2つの領域で当たり判定します。

これは点と長方形の当たり判定となります。
領域Aまたは領域Bに円の中心点が入っていれば当たりとなります。
領域A、Bの当たり判定の条件式は以下のようになります。

 
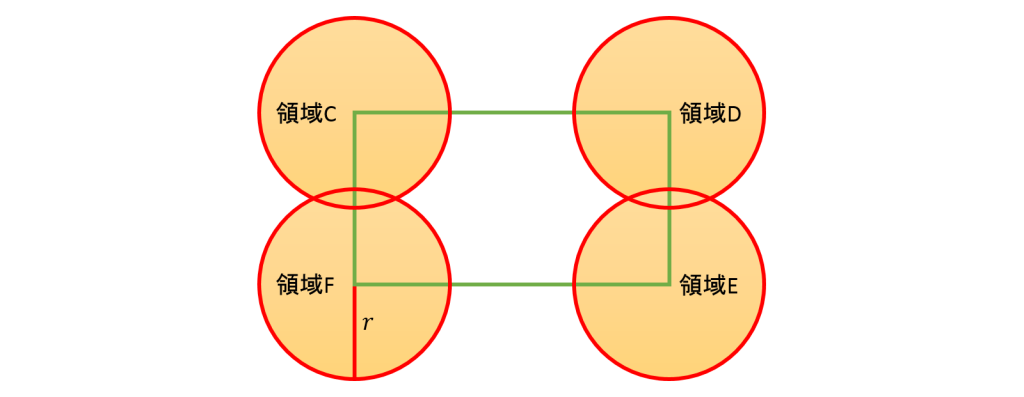
残りは角丸の当たり判定です。
これは以下のように長方形の各頂点との距離とすればよいでしょう。

したがって、領域C～Fの当たり判定の条件式は以下のようになります。

 
領域A～Fと円の中心点との当たり判定を行えば、一通りカバーできたことになります。
最終的に求めたい当たり判定の条件式は、領域A～Fの条件式の論理和で表せばよいため、以下のようになります。

 
円と長方形の判定では、条件判定回数が多く、計算が重くなります。
当たり判定を実装する際は、AABBを用いたブロードフェーズと組み合わせて使用するのが望ましいでしょう。
当たり判定の高速化 ‐ ブロードフェーズとナローフェーズ

今回のケースでは、円を辺の長さ2rの正方形（AABB）とみなして、まず長方形同士の当たり判定（ブロードフェーズ）を行い、当たった時のみ円と長方形の当たり判定（ナローフェーズ）を行う流れになります。

SOLID原則に従うなら、当たり判定の計算ロジックと高速化ロジックを分離して設計するのが望ましいでしょう。

 
円と長方形の当たり判定のやり方は他にも色々あると思います。
ひとつの考え方としてご参考にしていただけたらと思います。